
Equiangular triangle: A triangle having all angles of equal measure (Figure 7).īecause the sum of all the angles of a triangle is 180°, the following theorem is easily shown.Acute triangle: A triangle having all acute angles (less than 90°) in its interior (Figure 6).Obtuse Triangle- A triangle whose any one angle is obtuse angle is called an obtuse. The largest whole number L that works is 14'cm'. So the equal legs must have a length L such that L2+L22L2 must be less than (20'cm')2400'cm'2. In an obtuse triangle, the square of the longest side is greater than the sum of squares of the other two sides. Obtuse triangle: A triangle having an obtuse angle (greater than 90° but less than 180°) in its interior. It follows Pythagorean theorem, which you can study here. The other two sides each have a maximum length of 14 centimeters.Right triangle: A triangle that has a right angle in its interior (Figure 4).The types of triangles classified by their angles include the following: Scalene triangle: A triangle with all three sides of different measures (Figure 3).Isosceles triangle: A triangle in which at least two sides have equal measure (Figure 2).In Figure 1, the slash marks indicate equal measure. (1 point) acute, scalene acute, isosceles - right, scalene obtuse, scalene 2. Equilateral triangle: A triangle with all three sides equal in measure. What is the correct classification for the triangle shown below A triangle has two angles measuring 68 degrees and 22 degrees.The types of triangles classified by their sides are the following:
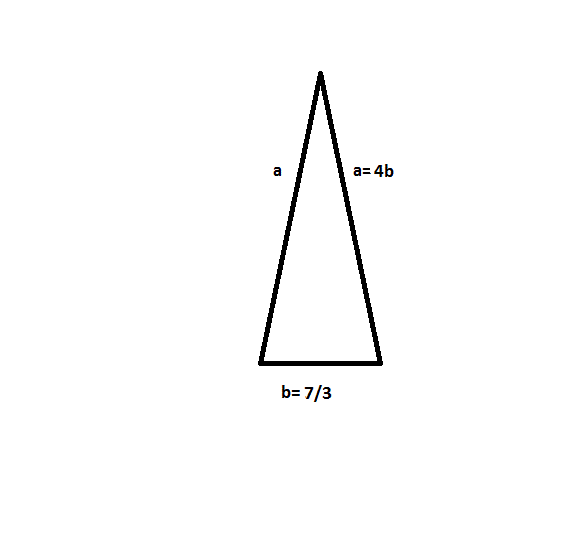
In an acute triangle, all angles are less than right angleseach one is less than 90 degrees. Concept: Classification of Triangles (On the Basis of Sides, and of Angles) - Isosceles Triangles. An obtuse triangle may be isosceles or scalene. An isosceles obtuse triangle with equal sides 5 cm. In an obtuse triangle, one angle is greater than a right angleit is more than 90 degrees. All of each may be of different or the same sizes any two sides or angles may be of the same size there may be one distinctive angle. A right triangle may be isosceles or scalene. Triangles can be classified either according to their sides or according to their angles. Summary of Coordinate Geometry Formulas.Slopes: Parallel and Perpendicular Lines.Similar Triangles: Perimeters and Areas.Proportional Parts of Similar Triangles.Formulas: Perimeter, Circumference, Area.Proving that Figures Are Parallelograms.Triangle Inequalities: Sides and Angles.Special Features of Isosceles Triangles.Classifying Triangles by Sides or Angles.Point c (triangle height not z.10 posts Another term I believe is the reference angle: ApWddeB.png. Lines: Intersecting, Perpendicular, Parallel I would like to make a third point c (position array).


 0 kommentar(er)
0 kommentar(er)
